Jupyter Notebook Cheat Sheet This Jupyter Notebook cheat sheet will help you to find your way around the well-known Notebook App, a subproject of Project Jupyter. You'll probably know the Jupyter notebooks pretty well - it's one of the most well-known parts of the Jupyter ecosystem! Karlijn Willems Jupyter Notebook Cheat Sheet September 19th, 2017 This Jupyter Notebook cheat sheet will help you to find your way around the well-known Jupyter Notebook.
- Jupyter Notebook Cheat Sheet Pdf
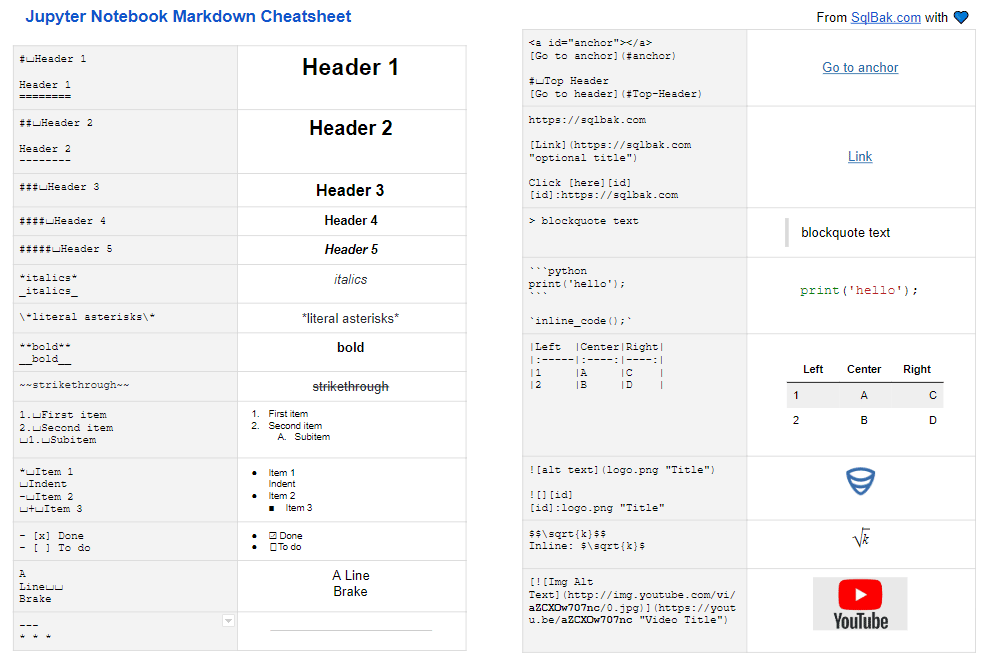
- Jupyter Notebook Cheat Sheet Markdown
- Jupyter Notebook Tutorial Pdf
- Jupyter Notebook Keyboard Shortcuts Pdf
This document will be available to you during tests and exams
7.1. Table of Contents¶
7.2. Numeric¶
7.3. Basic plotting functions¶
7.4. Symbolic manipulation¶
7.4.1. Imports¶
Symbol definitions
Example controller and system
7.4.2. Working with rational functions and polynomials¶
We often want nice rational functions, but sympy doesn’t make expressions rational by default
The cancel function forces this to be a fraction. collect collects terms.
In some cases we can factor equations:
Obtain the numerator and denominator:
Jupyter Notebook Cheat Sheet Pdf
If you want them both, you can use
Convert to polynomial in s

Once we have a polynomial, it is easy to obtain coefficients:
Calculate the Routh Array
To get a function which can be used numerically, use lambdify:
7.4.3. Functions useful for discrete systems¶
Write in terms of positive powers of (z):
Write in terms of negative powers of (z):
Inversion of the (z) transform
Jupyter Notebook Cheat Sheet Markdown
7.5. Equation solving¶
7.5.1. Symbolic¶
7.5.2. Numeric sympy¶
7.5.3. Numeric¶
7.6. Matrix math¶
7.6.1. Symbolic¶
Creation
Determinant, inverse, transpose
Jupyter Notebook Tutorial Pdf
Jupyter Notebook Keyboard Shortcuts Pdf
Math operations: Multiplication, addition, elementwise multiplication:
7.6.2. Numeric¶
Creation
Determinant, inverse, transpose
Math operations: Multiplication, addition, elementwise multiplication:
